bespoke geometry
Cocoon
Cocoon is an add-on to McNeel’s Grasshopper visual scripting interface for Rhinoceros. Cocoon is a fairly straightforward implementation of the Marching Cubes algorithm for turning iso-surfaces into polygonal meshes. It is geared specifically toward wrapping existing geometric elements, and works with combinations of points, breps and curves, allowing users to vary a number of parameters that enhance sculptural potentials. It is still rough (and there are definitely a number of other approaches to level sets and isosurfacing that are faster, more robust, more elegant, and/or have more potential) but due to time constraints related to other work I am doing – now and into the near future – I thought it effective and fun enough that it was worth it to make this available to the community. As such, though, general caveats apply: it’s probably easy to break, and it will definitely generate some artifacts. But please download and have a play, and feedback on the grasshopper forum is welcome. There’s a longer description after the break.
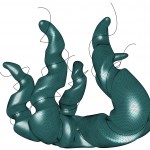
Cocoon reworks an earlier script – the Geometry Wrapper – that I had put on the forum some time ago. Like this earlier one, it is based on the marching cubes and implicit surface posts by Paul Bourke on his website. The lookup tables are directly lifted from his script, and the metaball calculations used here are directly pulled from his page. The first difference between Cocoon and the earlier script is that Cocoon breaks out geometry charges into individual components, which hopefully will make it easier to manage and control a variety of inputs. The second difference is that Cocoon also separates the radius of influence and strength of each charge into two parameters. This not only allows for slightly more nuanced control over how each charge behaves, but it also enables negative charges. I have definitely found playing with negative space quite a bit of fun. The next is that curve charges can be dynamically varied with much greater control. The geometry from following image is driven by only seven curves (two of which are procedurally generated corkscrews along the bottom):

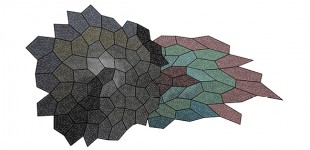
The rest of the variety is managed through the input of value lists for the strengths of the curve charges. The component reads multiple values and internally generates a spline which it uses to evaluate and assign charge values for points in the sampling grid. So however you feed a list of values into the charge, it will transform them into a basic law curve for dynamic assignment of charge values. Following is the definition for the above image. You can see it’s using gene pools, graph mappers, and some basic functions to adjust charge values along the lengths of each input curve.
The next change is that Cocoon splits out the solving of the marching cubes from a component that can then refine the mesh. This refinement is interesting in that even as it cleans up a good deal of the ugly triangulation and valence issues that plague marching cubes, it uses embedded charge information to project the mesh back to the target iso-value. Here I was influenced by Daniel Piker’s setup for his development of Æther, which to be sure is a more elegant approach to isosurfacing through voxels. (In fact, I looked into simply extending his work for this implementation, but I had some trouble keeping good control over the mesh – his use of gradients to move vertices back to the level set works perfectly, but it tends to move particles across faces, and resulting mesh faces and edges tend to overlap and clash. I expect that this can be adjusted, and perhaps moving forward – if I get back to working with level sets again – I may try to see what I can do to get it working properly, although I may also try my hand at some point at writing a wrapper for OpenVDB, which I just learned is open-source.) But for this more modest implementation, the mesh normals at each vertex and its re-calculated iso-values direct the mesh refinement. This component also works with half-edge mesh data structures, relying on Daniel’s and Will Pearson’s Plankton library, and also borrows a few techniques found in Daniel’s Mesh Machine, all of which can be found on Github.
The refinement of the mesh requires that you input the number of resampling iterations it should cap at, a unit of length for resampling, and a tolerance of variance from the target iso value that will satisfy the resampling goal. Basically, after each vertex is smoothed or subdivided, the resampling process tries to get it back to the target iso-value. The larger the sample size you set, the fewer iterations it should take to get back to that level…but it’s easy to “overshoot” here. For sure, this is where the script is most liable to break down and produce all sorts of artifacts. However, the overall refinement process produces much better results than the Geometry Wrapper.
The other big change is internal and has to do with how the sampling grid is managed. The key to the earlier scripts relative speed was its use of an RTree to limit the number of grid points that needed sampling. The problem with this I think is that it still had to generate the entire grid to begin with, so even with the speed of the RTree, very large grids created problems. Here, I’ve replaced this by first generating a base grid space, and then only populating cells wherever the charge geometries are located. In some instances, the former script is actually faster, but only marginally, and once you start to get into much larger grids, this approach speeds things up. It also helps that the marching cube solving is done using multi-threading.
Have fun!